Including Systematics

• Introduction
• The IBranchNamer class
• Usage Example

Introduction

The last remaining piece to add is the impact of systematic variations. A systematic variation is a common way of propagating uncertainties through an analysis. The effect of an uncertainty on a variable is evaluated by shifting its value by some amount (usually 1σ) and propagating the effect of this through the analysis. This then has a domino-like effect as variables and filters that depend on that variable must also be varied, and anything depending on those must be varied too (continuing down through the whole analysis chain).

The easiest way to evaluate this is to run the entire analysis several times, once per systematic variation. However, this is quite wasteful and requires running exactly the same systematic variation multiple times.

The Node class has an understanding of systematic variations built into from the start so allows a much more natural approach. Each Node contains a std::map from systematic names to ROOT::RDF::RNode objects. These represent all the systematic variations 'active' on that node. These systematic variations are all the ones that affected filters upstream of that node (and therefore may be seeing a different set of events to each other).

When a new operation is applied to a node the following sequence of steps occur

1. The set of input variables to the operation are determined
2. The set of systematic variations affecting these inputs is determined
3. For each active variation on the node the operation is performed
4. For each remaining systematic variation from step 2, the operation is performed on the nominal variation. For filters this adds more 'active' variations.

This behaviour is implemented by the RDFAnalysis::NodeBase::Act function (don't worry if you can't read the template syntax for this function, it's unlikely that you will have to interact with it directly).

Warning: right now this behaviour doesn't work quite correctly for filter calls using the variant where a decision and weight are calculated simultaneously. This variant is unable to tell which variations affect the decision and which affect the weight, therefore it assumes that each variations affect both of them, resulting in many redundant calculations downstream.

The IBranchNamer class

All of this is taken care of for you by the IBranchNamer class. This is an abstract interface that keeps a record of which systematics affect which branches. It is also able to convert between 'base' branch names (which are the ones used in all RDFAnalysis classes) and systematic resolved branch names which are used in all underlying ROOT::RDF::RNode calls.

The default version of this class is the RDFAnalysis::DefaultBranchNamer. This class assumes that all branches in your tree are of the form SystematicName_BranchName (or the same with the order reversed). The class is initialised with a list of systematic names to search for, if no systematic name appears then in a branch name then it is assumed that that branch belongs to the nominal variation.

Usage Example

To illustrate this, let's return to the Zγ example. Let's modify the original example to have three systematics: "GAM_KIN" which affects the photon kinematics, "ELE_KIN" which affects the electron kinematics and "MU_KIN" which affects the muon kinematics. The input tree now looks like

std::vector<TLorentzVector> NOSYS_Photons;
std::vector<TLorentzVector> GAM_KIN_Photons;
std::vector<TLorentzVector> NOSYS_Electrons;
std::vector<TLorentzVector> ELE_KIN_Electrons;
std::vector<TLorentzVector> NOSYS_Muons;
std::vector<TLorentzVector> MU_KIN_Muons;

The only difference to the code snippet to apply systematics is now in the creation of the root node. This now looks like

std::unique_ptr<node_t> root = node_t::createROOT(
    inputDF, //> The input to this analysis
    std::make_unique<RDFAnalysis::DefaultBranchNamer>({"NOSYS", "GAM_KIN", "ELE_KIN", "MU_KIN"}), //> Now initialised with all the systematic names
    false //> run without weights
    );

and the computational graph now generated looks like

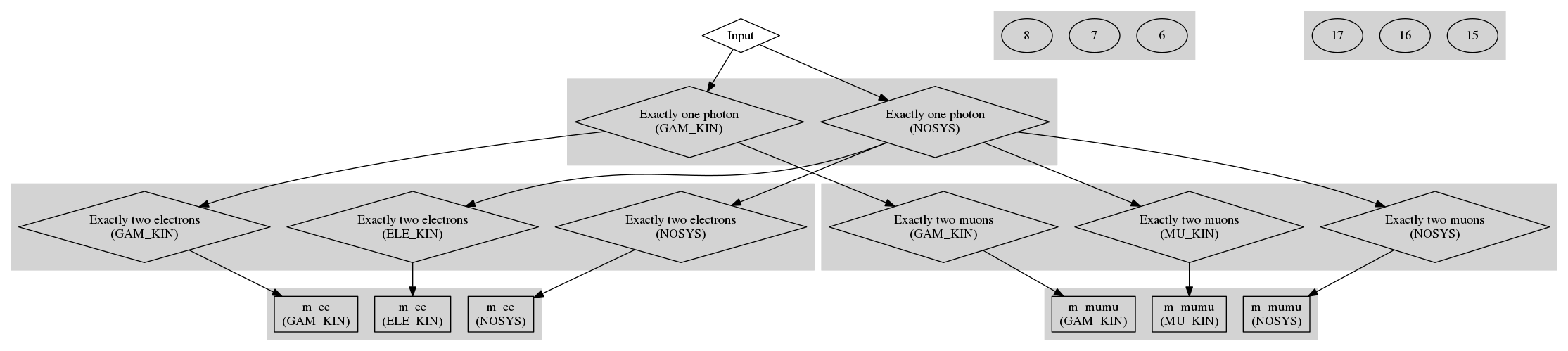
where systematic variations of the same node have been clustered together. Note how each variation is only applied where it is relevant!